How to efficiently represent strings using a Trie data structure
This post gives an introduction to the Trie data structure and explain how to efficiently use it to store and represent strings.
A trie, or a prefix tree, is a data structure that is used to represent and store a set of words. Although there are many other structures used to store and represent words, the trie is particularly efficient in performing the following operations:
- find all the words with a common prefix.
- enumerate the words in lexicographical order.
Thanks to these properties, tries have many practical applications like design an autocomplete word system, implement speel checkers or solve word games.
Introduction
A trie is a tree data structure whose nodes store the letters of an alphabet. Words can be retrieved from the structure by traversing down a path of the tree. The term “trie” comes indeed from the word retrieval and it is usually pronounced like “try”, to distinguish it from other “tree” structures.
The basic properties of a trie are:
- each path from the root to leaves forms a word;
- all the descendants of a node share a common prefix associated to that node.
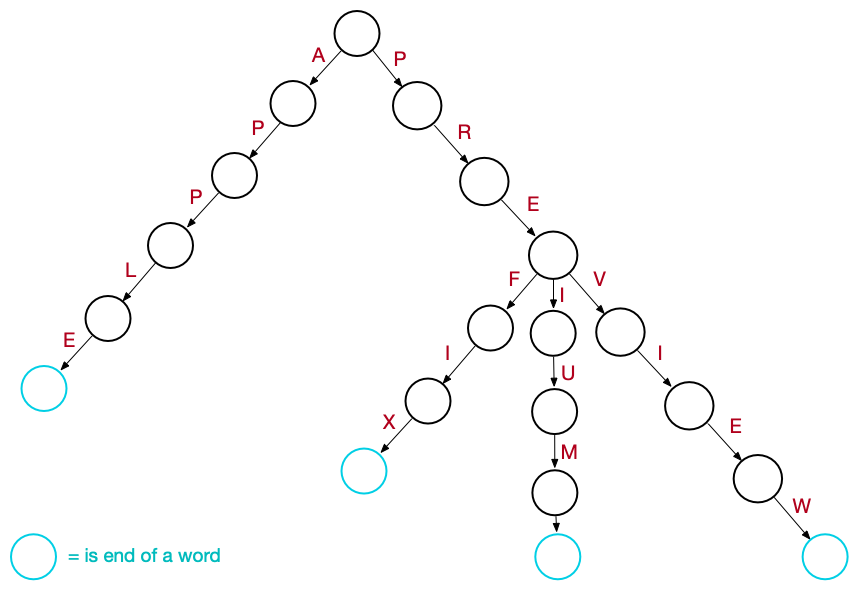
Each node stores letters as links (or references) to other nodes. There is one link for each possible alphabetic value, so the number of child nodes in a trie depends completely upon the size of the alphabet. The English alphabet has 26 letters, so the total number of children for each node will be 26. Since words share common prefixes, it is somehow necessary to understand where a word in the trie ends. A common solution is to associate to each node a boolean field which specifies whether the node corresponds to the end of a word.
Graphically a trie can be conviniently represented as a tree where each edge is labelled with a single character. So the first letter of each word is represented by an edge connecting the root to one of his children. The end of each word in the trie can be represented with colored nodes that are the endpoint of the edges labelled with their last character.
Trie Node
Each trie node contains the following information:
- a boolean variable isWord indicating whether a word ends in this node. It is convenient to initialize this isWord to false since the majority of trie nodes are not representing the end of a word.
- a set of links or references to other nodes. Commonly the links can be implemented using a fixed size array having as many element as the alphabet letters. This solution is usually very fast, but have the downside of taking up a lot of memory with empty links. The alternative is to use a map
with characters as the key and the link to the next node as the value. This is also the preferred way in dynamic programming languages like Python.
class Trie {
struct TrieNode {
vector<unique_ptr<TrieNode>> children;
bool isEndWord;
TrieNode() {
children.resize(26);
isEndWord = false;
}
};
unique_ptr<TrieNode> root;
//continue...
};
API Implementation
There are two basic operations provided by a trie: inserting a new word and searching for a given word.
To insert a new word, we need to iterate simultaneously through its characters and the trie nodes. Starting from the root node and the first character of the new word c, we check whether the root contains a valid link corresponding to c. If it is, we can directly move to the node pointed by the link and consider the next character of the new word as well. Otherwise we need also to create a valid link initiating a new node. Once we iterated through all the characters of the given word, we also need to check the boolean flag of the current trie node to true to indicate that word ends there.
void insert(string word) {
auto iter = root.get();
for (char c : word) {
size_t index = c-'a';
if (!iter->children[index]) {
iter->children[index].reset(new TrieNode());
}
iter = iter->children[index].get();
}
iter->isEndWord = true;
}
To search a given word, we proceed in a similar way iterating over its characters and moving along nodes and edges of the trie. The difference is of course that we don't create anything. If we try to move along an edge that doesn't exist, we simply return false. Once we iterated through all the characters of the given word, we also need to check the boolean flag of the current trie node to see if an already inserted word ends there. Clearly this last step shall be omitted if we want to verify the existence of a given prefix instead of a word.
bool search(string word) {
auto iter = root.get();
for (char c : word) {
size_t index = c-'a';
if (!iter->children[index]) return false;
iter = iter->children[index].get();
}
return iter->isEndWord;
}
Regardless of the number of words stored in it, the time complexity for both the operation is always O(W) when W is the length of the input word.
Comparison with other data structures
There are other data structures, like balanced trees and hash tables, that give us the possibility to store a dictionary of words and search for a word in it. So when do what are the advantages of using tries? First of all, as we mention during the introduction, such data structures are not efficient in enumerating the words in lexicographical order or in working with a common prefixes. For example a trie allows to efficiently answer to the following questions:
- Are there any words that start with a given prefix?
- How many words start with a given prefix?
- What are all the words that start with a given prefix?
Another reason to use a trie instead of a hash table, is because of potential memory advantages. When several strings have a common prefix, a trie reuses the same nodes and edges for all of them, saving space respect to an hash table that always increases in size. Moreover an hash table needs to deal with hash collisions and this could deteriorate its search time complexity. Of course, in the worst case, when all stored strings start with a different letter, there are no memory optimizations.
